4. The Hardware of Quantum Computers
Constructing quantum computers is an extremely daunting task. In the sections that follow, we will discuss the various components of a quantum computer and explain how we can build one by integrating different technologies that interact with the machine.
First, we will give an overview of the entire system and briefly touch upon all layers. Over the subsequent 4-6 chapters, we will delve deeper into the quantum chip (qubits) layer.
Each qubit necessitates the use of a specific material. These materials must contain particles suitable for creating the qubits while remaining uncontaminated by other particles. As a result, it is critical to ‘grow’ these required materials.
To fully grasp the concepts presented herein, we will need certain mathematical tools. The mathematical basics will be explained in the chapters on Ket notation.
Generally speaking, the ‘building blocks’ of a quantum computer include components such as memory, bus interconnect, and processor chips. Peripheral devices like keyboards or screens are essential for interacting with the machine.
In the following segments, we will discuss the broader aspects of a quantum computer: from programming it to interpreting the results. The first term we want to emphasize is compute. In reality, we are not merely building a quantum computer; we are developing a quantum accelerator. Specifically, we are creating a computational device that can be connected to a classical processor, which will then provide the performance required for various applications that are beyond the reach of classical computing. The concept of a heterogeneous multicore architecture offers a global view of our current understanding in this domain.
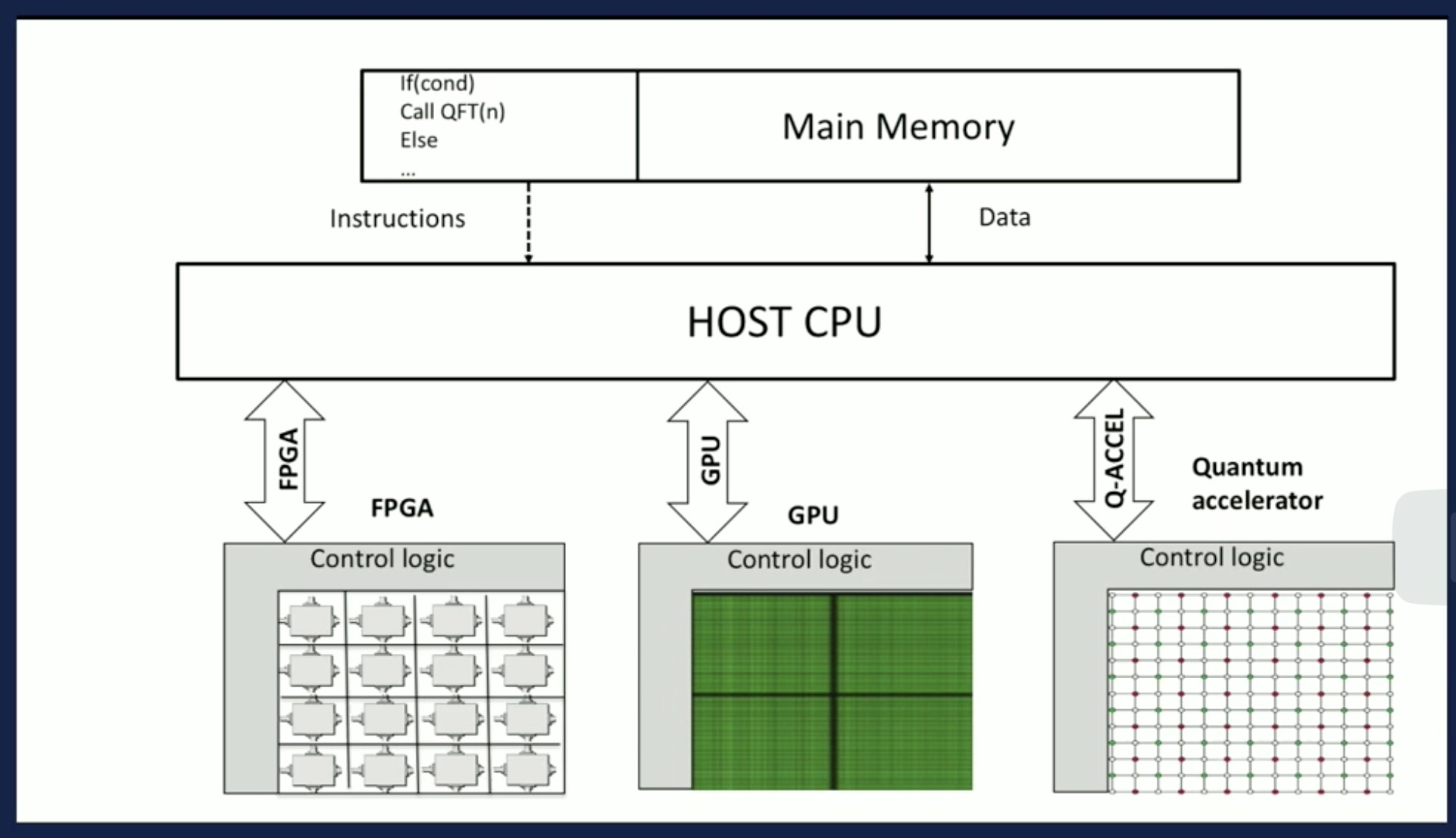
Heterogeneous because we have different kind of accelerator technologies. We have an
Field Programmable Gate Array (FPGA). We have
Graphic Programming Unit GPU’s. These are the vector processors we are using to produce graphics computation.
The third alternative accelerator technology will be a quantum co-processor which has the quantum properties that will provide a substantial increase in the compute power. This is basically what we see.
That also means that when you write any application, you will most likely end up using different kinds of accelerators including the FPGA, the GPU and also the quantum accelerator and therefore your application has to be compiled for four different instruction sets; namely, your
Intel processor for instance on the classical machine, your
FPGA instruction set, the
GPU instruction set, and also the
quantum instruction set.
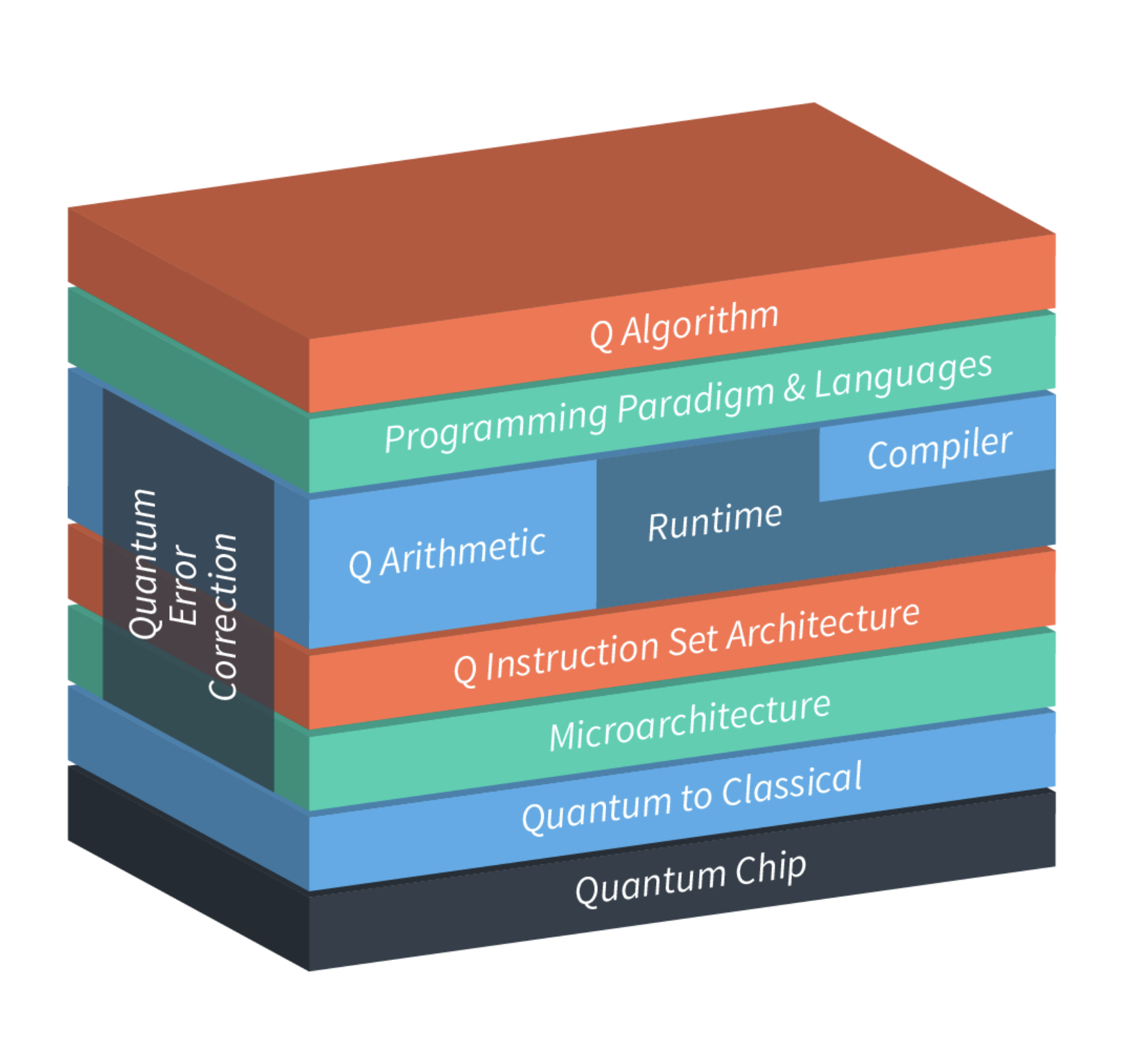
That is very important to understand, so whatever we are going to discuss in the following talks is only going to focus on the quantum accelerator device or the application processes that we need classically as well as quantumly to be provided
Whenever we talk about a computer, classically we have divided that in different layers; the lowest layer is always let’s say the hardware, the
chip that has been designed. It is never a single chip or a single processor.
(Quantum to Classical) No, it has memory, it has interconnections, so a bus that allows the processor to communicate with the memory to retrieve instructions and to retrieve or produce the data. And then it goes up to the
Microarchitecture that we need, up to the application level. We will now go in detail on each of those layers in a quantum context. Because we are basically adopting the same kind of layer view of what a quantum accelerator or a quantum computer would be, and we simply put the Q of quantum in front of every layer. And that is our research and working program. The highest level is the 7 (4) quantum algorithm that we know of. We don’t even know yet what they will be. We have examples such as factorization that is used in cryptography in securing communication between machines.
But quantum algorithms can as well be designing a new molecule for personalized medicine. It can be that you might want to have a climate module that you want to run on your quantum accelerator that take all kind of mechanisms into account that we currently are unable to compute or even model on a classical machine. So that is the quantum algorithm layer, and that is where the biggest opportunity lies worldwide. Where many companies and organizations can actually start developing their own quantum application. Because every company or every end-user can think of how they can use that computational aspects of such a device.
One layer lower is that when you have an application that you need to program. You do that classically again. You have a programming language such as C++, Fortran, Cobol or any language that you can think of. Those languages can produce the code for a classical processor. But we also have to develop our own quantum language for the quantum accelerator. There are a couple of languages that have been developed so far. There is ScaffCC, and ProjectQ. And here at QuTech we are developing our own programming language called OpenQL, which is inspired by OpenCL, which is a language developed for GPU programming. We are now shifting it to the quantum infrastructure, so making the changes to that language. So that is the programming language layer.
For every programming language we need a compiler. A compiler takes the input of your algorithmic logic and compiles it into a lower level language that is classically called an assembly language. Again here we are working on a quantum assembly language which we call QASM, which was originally developed for a book ‘Quantum computation and information’ by Nielsen and Chuang. To generate the figures in their book of the quantum circuits.
We just expanded that language into a full-fledged quantum assembly that is being generated by our OpenQL compiler, which is the programming language that we also developed. So that you can express your quantum logic in such a way. We are internationally collaborating with other partners working on similar things such that we standardize this quantum assembly language. Because for now everybody has its own local version, and that is not very good that everybody has his own variation, but if we all agree that this is what we assume to be QASM, then progress will come much faster.
The next layer is quantum arithmetic’s because the mathematics of what you need to do is completely different than classically. The quantum gates operate quite differently, that’s why you need to develop the quantum arithmetic; how to do a quantum operation. I will not say anything about run-time, which is another part that we need in a quantum accelerator. Because we will need it, but what kind of functionality it should have is a bit unclear right now. That is where there is the tension between the compiler development because we still can develop a lot of things in the compiler and maybe at a later stage we will develop that in a run-time support.
All of this QASM basically maps very well one on one with the quantum instruction set. This quantum instruction set basically describes what the operations are that your quantum device is capable of executing. That is why we have to think of what these instructions are. We know that classically we use an assignment like A = B + C. We should be able to do something similar in a quantum device. But it is not as simple as retrieving data from a memory location and perform the addition and writing back the result, because in quantum we use qubits.
A qubit is a quantum bit. Classically, we reason in terms of bits, zeros and ones. And as you know we are now using qubits, quantum bits. And they can be also zero or one, but they can also be zero and one at the same time. And that is the famous superposition that we are exploiting in a quantum device. We can also combine two qubits so we don’t have two different states but we have a combination of those states; namely 4 states at the same time.
we have 2^3 = 8 states. Now what is very nice about quantum is that the quantum mechanics gives us parallelism for free. Because I can apply quantum gates on those 2^n different states. You will come to understand in the upcoming lectures that nothing really comes for free. There is still a lot of challenges that need to be resolved. But that is ultimately the big challenge and the big opportunity that quantum offers. That is why you have to understand what this instruction set is and the corresponding architecture should be. And that immediately brings us to the layer of the micro-architecture.
Just like any classical processors we have also a quantum micro architecture for my quantum device, which contains the processor, the memory and also the interconnects of how the processor will communicate with the qubits. It has local registers in the processor and an ALU, an arithmetic logical unit so that it can compute logical and arithmetical operations, and write back the result to memory so that the user gets an idea of what the algorithm has computed as a result.
So again here in the quantum case we have a micro-architecture which has a similar kind of functionality. And that is the one we are also currently implementing in a real device that already controls a number of the physical qubits; a superconducting as well as a spin qubit that we are developing at QuTech. For now we are working on a 17 qubit micro-architecture, so that in principle we can go up to 2^17 parallel executions on the combination of those 17 qubits.
A layer lower is the quantum to classical layer. Because whatever you perform on the quantum level is always an analog phenomenon. Now you say; “analog? I thought we were building a computer? Which should be digital…”. Well, everything up to the micro-architecture is clearly digital, but ultimately what you send down to the quantum chip is for example a microwave, it can be other things, but let’s say it is a microwave and we control an individual electron at the atomic level. The individual electron is important to understand. So if I have 17 qubits, I basically have 17 electrons, not hundred thousands, not millions, but 17. And there are ways to combine those 17 electrons and their spins in the way that they interact and move that indicates that they are doing a particular calculation. So that means that this layer is necessary for translating all of the logical steps that you need to do in your algorithm into the appropriate microwave or the physical signal that you want to send to this electron and to the qubit.
And then ultimately it enters into the quantum chip. Which consists of these qubits which are connected to each other. And then we hope of course that we get a meaningful result. Now it is never the less important to understand for a quantum accelerator for any computational device is that it is a non-deterministic way of computing. That means that it is not like in a classical machine that you run a thousand times exactly the same algorithm and you will get a thousand times exactly the same result. Quantumly this is absolutely not true, because when you want to read out the result several things happen. The most important is that any entangled superposition that exists, actually is going to get destroyed. So if I have for example 2^17 possibilities, I am only going to get one of those possibilities back as a result. And all the others will disappear.
And that is why you maybe have to do a computation 10 times, maybe 100 times, we don’t even know how many times we need to do that. And then you can make a histogram of what has been computed, and the readout that has the highest frequency of occurrence has a high probability of being read out by our micro-architecture and that is what we can report back to the end user. So that is something that you should not forget. A quantum device is a very powerful device, it gives massive parallelism in principle. But we need multiple runs and average out what those calculations of those results are. And the one with the highest frequency is the most likely result of your quantum device.
Main takeaways
Current efforts are put into building a quantum accelerator, a computational add-on to the classical computers to exceed current performance.
Heterogeneous multicore architecture entails a Field Programmable Gate Array, a Graphics Programming Unit and a quantum co-processor.
The building blocks for a quantum computer are a quantum algorithm, a quantum language, a compiler, arithmetic, an instruction set, a micro-architecture, a quantum to classical conversion and a quantum chip.
Q1
When N classical bits are read out after a computation they can be found in one of \(2^{N}\) different states (e.g. if you read out 2 classical bits from your computer’s memory you will find them to be 00, 01, 10, or 11). When N qubits are read out after a computation they can also be found in one of \(2^{N}\) different states, just like classical bits. Where, then, does the advantage of using a quantum accelerator for some tasks come from?
There is no advantage to using a quantum accelerator.
Unlike the classical bits, which can be in only one of the 2^{N} states before the read-out, the qubits can be in a superposition of the 2^{N} states (i.e. they can be in all 2^{N} states at the same time) before the read-out.
A quantum accelerator uses the spin of electrons as the unit of computation. Since electrons are smaller than the transistors used in classical computers, quantum accelerators are faster. unanswered
Q2
“Quantum parallelism” is a term that is sometimes simplistically used to refer to the fact that when using N qubits in superposition to do computation it is as if we are doing 2^{N} computations at the same time. What is the main reason this can be misleading?
While we can do operations on all the constituent states of a superposition simultaneously, we can only ever read out a single one of those states.
Qubits are much more difficult to work with than classical bits, and so we can’t really claim to be able to do computations on them.
It should be “ computations at the same time” instead of “ computations at the same time” because we only have qubits. correct
4.1. Quiz 1
In the previous we described the current design of a quantum computer. It is not quite a ‘quantum computer’, but rather a classical computer with an extra component that is capable of doing quantum computations; the so called quantum accelerator. With this design, the computer is capable of doing both classical and quantum computations.
4.1.1. Question 1: Designing the quantum computer
Why is it a good idea to use this design?
By using this, there is no need to reinvent the ‘wheel’ of computers.
There is a clear classical/quantum boundary. Classical computers can do certain computations that quantum computers cannot.
Typical classical parts of a computation can be performed on the classical part of the computer.
Since classical computers are many years ahead in development, this will be a lot faster.
Correct: A quantum algorithm typically has classical parts as well. A good example of this is Shor’s algorithm for semiprime factorization.
Explanation
We can use the classical design of a layered structure as a basis on designing a quantum computer. This design has been studied and optimized for years, there is no need to reinvent that wheel. Quantum computers are not always faster than a classical computer, contrary to popular believe. For some (most) tasks a classical computer would be just as fast or faster than a quantum computer. Then the classical computer is preferred as it makes less errors.
4.1.2. Question 2: Quantum Algorithms: beyond a speedup
Quantum computers are supposed to be a lot faster than classical computers for certain computations. We will soon dig into it, including what we mean by ‘fast’ and why quantum algorithms can have these properties. It is good to understand that by ‘fast’ we don’t mean ‘twice as fast’ or even ‘100 times as fast’. With the quantum speedup, we mean the difference between a month and the lifetime of the universe. So, computations that are nowhere feasible on a classical computer, suddenly become so on a quantum computer.
It is also good to think about whether quantum algorithms can do other things better.
Is there a computation that is, in principle, only possible on a quantum computer?
Yes
No
Explanation
Although it is highly inefficient (e.g. it would take decades), a classical computer can simulate a quantum computer. So everything that runs on a quantum computer can be simulated by a classical computer. Note that this does not apply to a quantum internet!
4.1.3. Question 3: A programming language for a computer
What does a programming language do?
A programming language is used to automatically schedule events (also called a program) of what the computer does.
It provides an extra layer between the computer and the user, so that the user can instruct the computer in an human-readable and understandable format.
It is an essential layer of a computer, without a programming language we cannot make a computer function.
Explanation
Without a programming language, every input into the computer would need to be an exact instruction on the CPU. This would make using computers very hard and would take a lot of time.
4.1.4. Question 4: The compilery
What does a compiler do?
It translates the instructions written in the programming language into something that the computer can actually use.
It does the same as a programming language, but only in an automated way.
It provides an extra layer, to ease the transition of user input to instructions that the computer can work with
Explanation
Without the compiler, the computer doesn’t understand the instructions. So, a compiler and a programming language go hand in hand!
4.1.5. Question 5: The current bottleneck
To design a complete quantum computer is no easy feat. There are still many problems and hurdles to overcome before a quantum computer becomes something that is widely available. There are problems across all layers of the design, but there is one layer that has the bulk of all the problems. It forms the current bottleneck of the technology.
What layer is that?
Quantum algorithms
Programming paradigm and languages and the Arithmetic, Runtime and Compiler
Quantum instruction set architecture
Quantum Chip
Microarchitecture
Quantum to Classical
Explanation
Without the compiler, the computer doesn’t understand the instructions. So, a compiler and a programming language go hand in hand!
In the following, we will see multiple designs of a quantum chip.
5. Quantum materials
Quantum materials are an essential feature if one would like to build a quantum computer or use the quantum internet. On a daily basis, Giordano Scappucci is working on optimizing quantum materials at QuTech. He will introduce you to this field of quantum mechanics.
Quantum mechanics describes how atoms bind and electrons interact at a fundamental level. Naively speaking, all materials are quantum because all matter, in the end, must be explained by quantum mechanics. For example, our body is largely made up of water. In water, chemical reactions bind hydrogen and oxygen atoms together. Although this can be explained by quantum mechanics, we usually don’t think about water in these terms, and a high-school-level chemistry description does the job. This is, because we can often approximate the quantum behaviour in materials by a classical description. It turns out that a classical description is in fact suitable for most of the phenomena that we experience in the macroscopic world around us.
Sometimes, however, to fully understand the behaviour of certain materials, it is necessary to keep quantum in view: there is no classical explanation to help our understanding. A feature of the broad category of Quantum Materials is that their behaviour is generally rooted in the quantum world. And while behaviours observed in quantum materials cover a wide spectrum, there are some common features that recur.
For example, many quantum materials derive their properties from reduced dimensionality. Electrons trapped in 2, 1, or 0 dimensions have different characteristics than electrons in 3D. Emergence is another recurring theme across quantum materials. Phenomena emerge due to the collective behaviour of original constituents.
In superconductor materials, the interaction between electrons, mediated by vibrations of the crystal lattice, creates the so-called Cooper pairs. Differently from individual electrons, Cooper pairs can share the same quantum state. Superconductivity emerges from the concerted state of pairs that propagates without electrical resistance through the crystal. Certainly, you need quantum mechanics to understand this!
The first quantum revolution, with the development of quantum mechanics, provided a microscopic understanding of nature. It had a tremendous impact in our life. Once you understand the periodic table and electronic wave functions, you understand semiconductors and how transistors are built and work. We now carry around billions of transistors in our pockets to perform complex tasks. It is clear that we need the concept of the photon to understand the laser.
We are currently in the midst of a second quantum revolution, in which quantum matter is engineered to develop disruptive technologies beyond the reach of classical understanding. Quantum computing is the man on the moon goal of such second quantum revolution. By working in a fundamentally different way, quantum computers have the promise of solving complex problems that classical computers cannot handle.
Quantum materials provide the environment where qubits, the elemental unit of quantum information processing, are defined and live. Therefore, quantum materials are at the basis of a quantum computer. To have a working quantum computer you need to couple together many qubits, while maintaining their long coherence time. These requirements are often conflicting. Qubits that are hard to couple together have long coherence times, because they tend to be isolated.
On the other hand, systems that are easy to couple together tend to lose coherence quickly, because they can be perturbed easily by the environment. In all cases, the precision of the qubit materials is crucial to solve these two challenging requirements. And when we say “precision”, we mean precision in terms of: materials uniformity, chemical composition, and electrical properties.
Ultimately, to make the phenomenally large number of qubits necessary to build a quantum computer, we would like to use the same manufacturing techniques of the microelectronic industry. Chemical vapour deposition, or CVD, is an industrial process that uses high purity gases to make high quality materials, with desired physical and electronic properties. For example, by depositing layers of silicon and silicon-germanium, we can tune the lattice parameter of silicon to be larger than usual and match that one of silicon germanium. As a result, the electronic properties of such hetero-structure, which is made of different materials, make it possible to form a 2D electron gas at the interface between silicon and silicon-germanium.
Qubits can then be made by isolating with electric fields one electron spin at that interface. If you want to isolate one single electron spin and make it a qubit, you need to know the properties of the host material very well. Once we make our crystal into a silicon heterostructure, we usually break it, and have a close look at it from the side with a high-resolution electron microscope. We call this microscope a transmission electron microscope, or TEM. Its working principle is based on electronic diffraction, another quantum effect, of an electron beam passing through a thin piece of material.
The spatial resolution is so high that we are able to see atomic arrangements in the lattice. In addition, a TEM is capable of distinguishing different elements from each other by their atomic weight. Therefore, it is a useful tool to analyze materials composition. Light elements appear darker than heavy elements. This allows us to check precisely to what extent, the material we made matches our expectations. For example, you see here the perfect atomic arrangement of silicon and germanium atoms at the critical interface between silicon and silicon-germanium. The lattice spacing is exactly the same at both sides of the sharp interface, indicating that the CVD process successfully strained silicon to match the underlying silicon-germanium.
The fact that we are able to make crystals with such precision and very little imperfections, is a key asset to then make good qubits. Once we know how the material we made looks like, we usually study its electronic properties, by modifying them with external parameters. Temperature, electric fields, and magnetic fields are the few knobs that we turn in our labs to probe quantum materials. These studies provide useful feedback to make the material a better environment for the qubits.
Take, for example, the Si heterostructure mentioned earlier. If we cool it to the very low temperatures at which qubits usually operate, say below one degree above absolute zero, it would be insulating. However, we can make the material conducting by imposing a vertical electric field. The electric field forms a metallic channel at the interface between silicon and silicon-germanium, which is then populated by electrons. The higher the electric field, the more the electrons in the channel.
By studying how the electrical resistance of such channel responds to a magnetic field, we are able to measure the number of electrons in the channel and their mobility. The mobility tells us how fast electrons can travel in such channel, and is an indication of the disorder in the system. The higher the mobility, the lower the disorder, and there will be a better chance of fabricating many qubits with similar properties. Materials homogeneity is one requirement to scale up the number of qubits into a quantum computer. Think of the billions of transistors in your laptop, if they were all behaving differently, there would be no chance of having them to work for you. And while we are currently optimizing quantum materials to build a quantum computer, ultimately, the hope is that when such a machine will exist, one of the first uses will be to efficiently simulate quantum systems, fulfilling the vision put forward by Richard Feynmann more than 30 years ago. In turn, this will help us understand and build even more complex quantum materials with extraordinary properties that today we cannot even predict.
5.1. Main takeaways
Quantum materials provide the environment where qubits, the elemental unit of quantum information processing, are defined and live.
Precision in material uniformity, chemical composition and electrical properties are crucial for the requirements of having both many qubits and long decoherence times.
Chemical Vapour Deposition is an industrial process that uses high purity gases to make high quality materials, with desired physical and electronic properties.
Transmission electron microscopy is a process to inspect the fabricated heterostructures with high resolution.
Temperature, electric fields and magnetic fields are useful parameters to determine properties of quantum materials such as mobility and electron density.
5.1.1. Material Criteria test quizz
A quantum computer should have some necessary properties to be called a quantum computer. These are called the DiVincenzo criteria:
The system must be scalable with well defined qubits;
The computer must have the ability to initialize the state of qubits;
Qubits must have long decoherence times;
The computer must be able to perform a universal set of quantum gates on the qubits;
It should be possible to measure the qubits.
We have to keep those criteria in mind when we choose the material for our qubits. For example, having homogeneous materials makes it possible to scale the system easily.
What property should the material have to ensure long decoherence times?
Use materials with low density where qubits can easily be accessed for error correction.
Use materials with high density to reduce the interaction of qubits with neighbouring qubits.
Use materials that can be cooled down quickly.
Avoid materials with a complex structure, as it is more likely to interact with the qubits.
Microarchitecture
Quantum to Classical
Explanation
It should be avoided that the material the qubit live in interacts with the qubit. If a material has a complex structure it is harder to avoid these interactions
Hint (1 of 2): What causes decoherence?
Hint (2 of 2): Qubits decohere when they interact with the environment Next Hint
5.1.2. Question 1: The usefulness of Cooper pairs
Cooper pairs can, unlike single electrons or other fermions, be in the same quantum state.
The invididual particles in the pair are fermions (both spin-1/2 particles), but the pair together is a boson (The total spin of the pair is 0 or 1).
How are cooper pairs created in superconducting materials?
The crystal lattice doesn’t allow single electrons to pass through the lattice, only pairs. So all electrons passing through the lattice are parts of Cooper pairs.
Moving electrons cause vibrations in the crystal lattice, which exert forces on other electrons, creating Cooper pairs.
The gravitational force between two electrons trap them in their gravitational wells, creating a pair.
Since Cooper pairs are bosons, bringing any two photons (or other bosons) together also is a boson, which is a Cooper pair.
5.1.3. Question 2
Where
\(\lambda\) is the de Broglie wavelength of the particle,
\(h=6.6*10^{-34}\mathrm{~J}.\mathrm{s}\) is the Planck Constant,
\(m\) is the mass of the particle.
For an electron ,\(\ensuremath{m=9.1*10^{-31}\mathrm{~kg}}\) and \(v\) is the speed of the particle.
The atomic structure has a size of \(100\) picometer \(\ensuremath{\left(=10^{-10}\right.}meter\ensuremath{)}\).
What is the minimum electron velocity that enables to image the material?
10^{4}\mathrm{~m}/\mathrm{s} - [x] \sim10^{7}\mathrm{~m}/\mathrm{s}
\sim10^{10}\mathrm{~m}/\mathrm{s}
\sim10^{13}\mathrm{~m}/\mathrm{s}
Explanation
\ensuremath{v>\frac{h}{m*\lambda}=\frac{6.610^{-34}}{9.110^{-31}10^{-10}}=710^{6}\mathrm{~m}/\mathrm{s}\simeq10^{7}\mathrm{~m}/\mathrm{s}}Thisisabout\ensuremath{10%} the speed of light. Analysing the material with light would require a wavelength of light in the X-ray region. ?
Hint: The speed of light is 299792458\mathrm{~m}/\mathrm{s}\left(\sim10^{\wedge}8\mathrm{~m}/\mathrm{s}\right)
Explanation A higher temperature means more particles are moving around in the semiconducter, bumping into the electrons, slowing them down. Changing the electric field doesn’t change the mobility, only the (drift) velocity.
5.1.4. Question 3: Mobility
The higher the mobility in a semiconductor, the smaller the disorder.
Which of the following can be done to best increase the mobility?
Decrease the temperature from room temperature down to 4 Kelvin.
Increase the number of impurities in the material. - [ ] Increase the electric field. correct
Which of the following can be done to best increase the mobility?
Hint (1 of 3): When is your car ride on a highway as smooth as possible?
Hint (2 of 3): Remove other cars with different velocities from the highway, and remove any potholes - Hint (3 of 3): The speed you’re going does not make the ride more or less smooth
6. Introduction to Ket notation
Before we dive deeper into the different layers of a quantum computer, we first want to introduce you to ket notation. Ket notation is a specific quantum method used to perform operations and measurements and will introduce the basics of ket notation.
Note that this is a densely packed section and don’t expect to understand everything after the first viewing. Much more time is needed to grasp the basics of Ket notation, and we advice you to review the following passages. Please do not let this subject deter you from following further. It is crucially important to understand the basics, because that will be used in the continuation. This is a difficult topic!
Typo:
$\mid \psi\rangle=\cos(\theta/2)|0\rangle+e^{i\phi}\sin(\theta/2)|1\rangle$
The highlited line should read: $\(\frac{1}{\sqrt{2}}(|0\rangle\langle0\mid0\rangle\otimes I|0\rangle+|0\rangle\langle0\mid1\rangle\otimes I|0\rangle+|1\rangle\langle1\mid0\rangle\otimes X|0\rangle+|1\rangle\langle1\mid1\rangle\otimes X|0\rangle)\end{array}\)$
We would like to control quantum degrees of freedom in order to implement quantum computing, among other goals that we have. To talk about these degrees of freedom, we’re going to use some notation that you might not be familiar with, but it’s all very close to linear algebra. You are likely already familiar with linear algebra, which has column vectors denoted with an arrow, or with boldface type.
Column & row vectors: $\(\vec{x}=\boldsymbol{x}=\left[\begin{array}{c} 10\\ 11\\ 12 \end{array}\right],\,\,\,\vec{y}^{T}=\boldsymbol{y}^{T}=\left[\begin{array}{ccc} 1 & 2 & 3\end{array}\right]\)$
It also has a transpose operation that maps column vectors to row vectors, and vice versa. We can calculate the inner product of two such vectors, either by transposing one of them and multiplying, or by writing the dot product explicitly. Either way, we get a scalar by taking the inner product of these two vectors.
In addition, we can transform one vector into another using a matrix, which can be written using boldface type or a hat, your preference.
There is a slightly different notation that we use for vectors and matrices in quantum computing, which we often call ket notation.
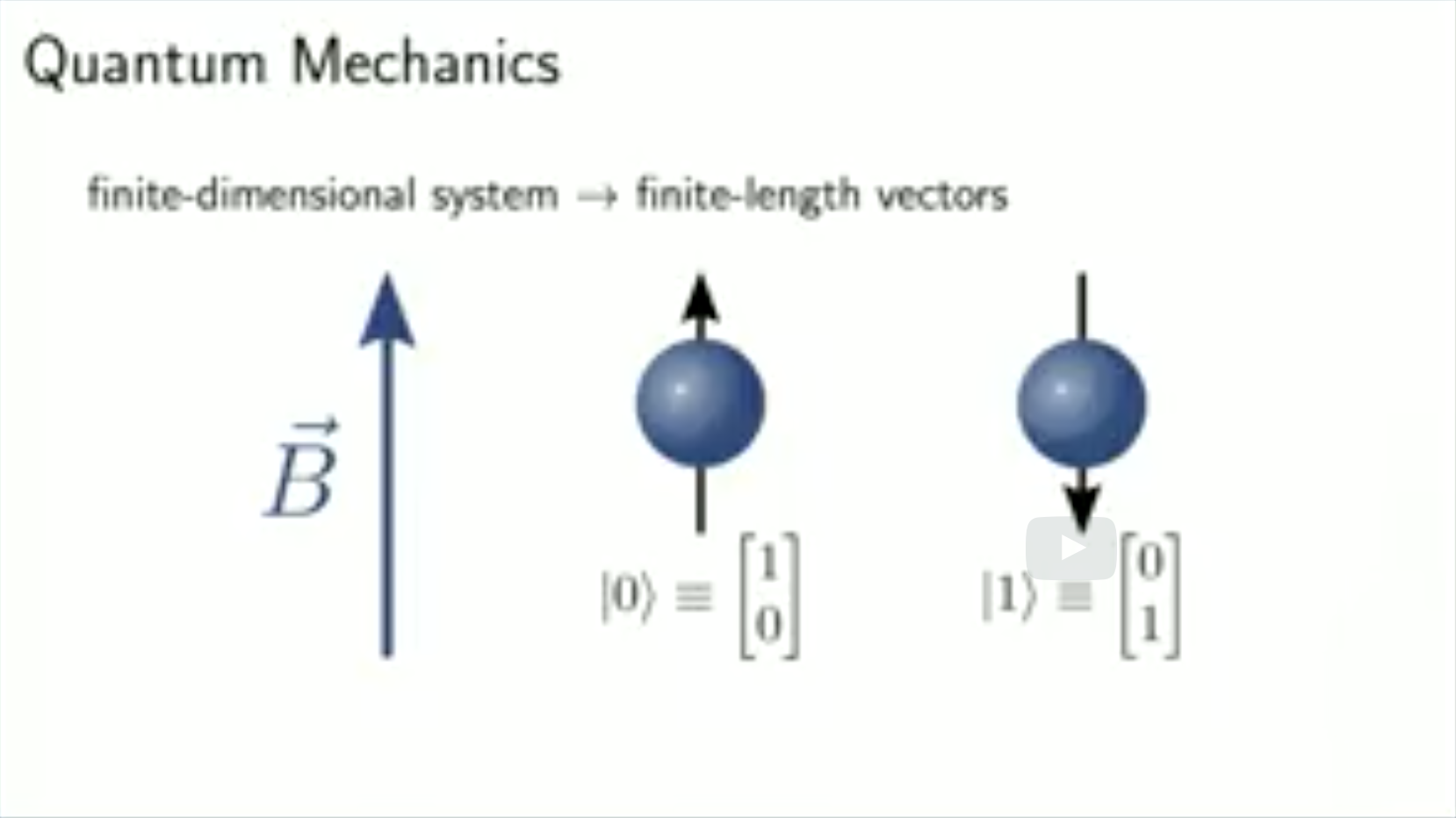
In ket notation, a quantum state is expressed using a column vector with complex coefficients. For example, we can express the state of a qubit, a two-level system, as a linear combination of two basis vectors, which we call 0 and 1.
Column vectors $\(\rightarrow kets:\mid\psi\rangle=\alpha\mid0\rangle+\beta\mid1\rangle=\left[\begin{array}{c} \alpha\\ \beta \end{array}\right]\)$
In a departure from regular linear algebra, there is a well-defined dual vector for each quantum state, called a bra, which we can obtain by taking the complex conjugate and the transpose of the ket vector.
Dual vectors $\(\text{Bra:}\langle\psi\mid=\left[\alpha^{*}\beta^{*}\right]\)$
This is important for calculating inner products, which we always do by multiplying the bra for one state by the ket of the other, forming a bra-ket.
Inner products:
A central feature of quantum mechanics is that, when we perform a measurement to determine whether a state is \(0\) or \(1\), for example, we get a random answer, and the probability of measuring a state to be \(0\) is given by the squared magnitude of its \(0\) coefficient.
One consequence of this is that, since such a measurement on a qubit state must result in \(0\) or \(1\), these squared magnitudes must sum to \(1\), since they are probabilities. This is called Born’s rule and the constraint that the probabilities must sum to \(1\), is called normalization.
Normalization:
We can also express qubit states in different bases. Consider the often-used plus-minus basis, which consists of the normalized sum and difference of the 0 and 1 ket vectors. Given a state expressed in the 0/1 basis, we can calculate the coefficients required to express the same state in the plus-minus basis, as I have done here.
States can be expressed in different bases:
This leaves us with a small question: if any basis is just as good as any other, is there a basis that we should use as the default? Fortunately, the devices that we use to store and manipulate qubit states provide us with just such a default basis.
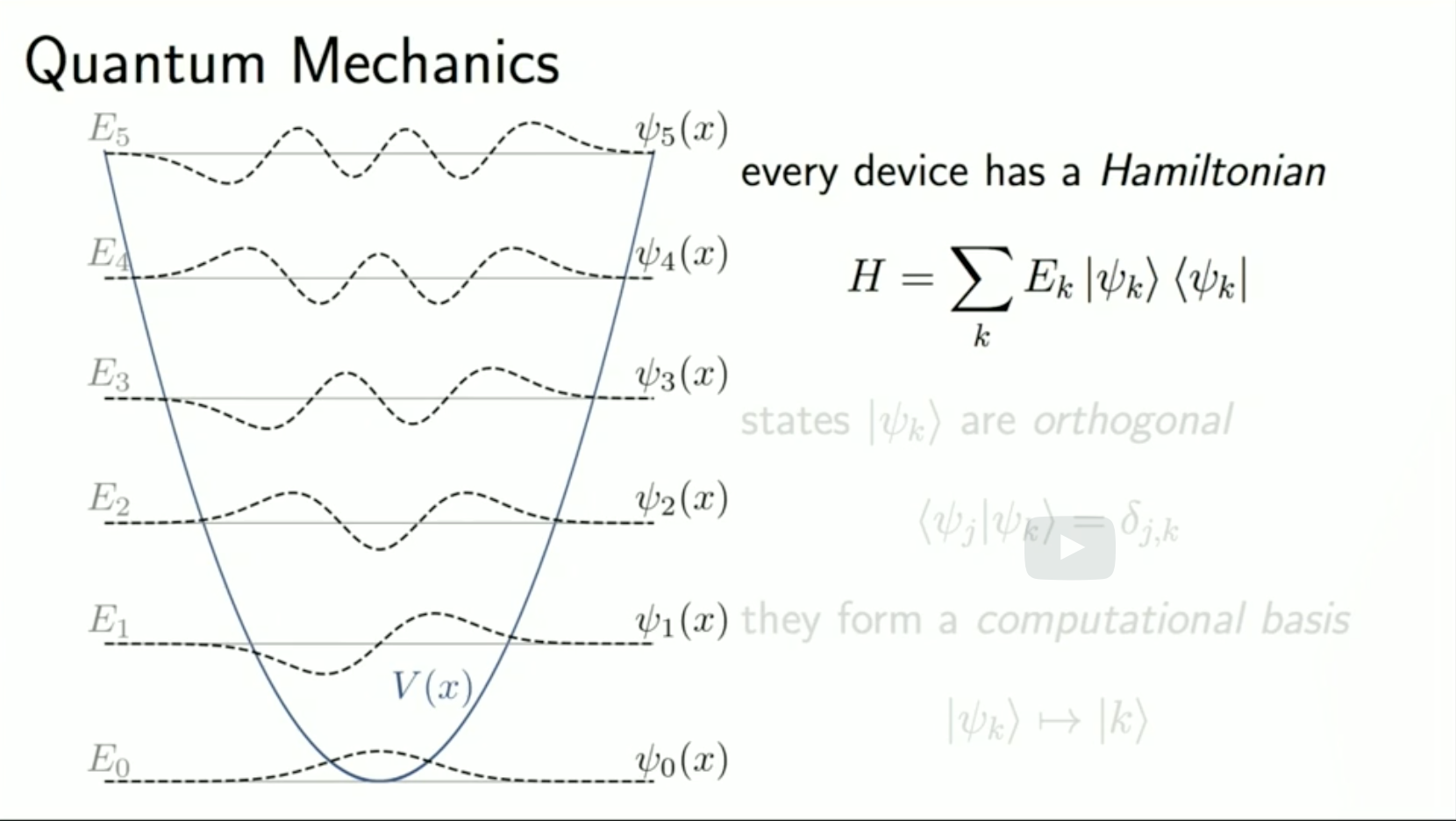
One such device, which we see quite frequently in quantum mechanics, is the harmonic oscillator, shown on the left. These devices are described by a Hamiltonian, which is a matrix that assigns an energy E_k to each of its eigenstates, or preferred basis states, psi_k.
Every device has a Hamiltonian:
These states \(\mid\psi_{k}\rangle\) are orthogonal:
and normalized (so we say that they’re orthonormal), so the inner product of \(psi_j\) with any \(psi_k\) other than itself is \(0\).
This allows us to use these states as a computational basis, replacing any detailed knowledge of the wavefunction psi_k with a simple label k that indicates which state we’re talking about.
They form a comutational basis
\(\mid\psi_{k}\rangle\mapsto\mid k\rangle\)
Some devices have finite-dimensional state spaces, unlike the harmonic oscillator.
6.1. Operations & Observables
Logic gates \equiv unitary matrices \(\equiv\) changes of basis
The logic gate is the smallest classical computing system, and all classical computations can be expressed as a large sequence of these gates. The quantum counterpart to a logic gate is a unitary matrix, which replaces the computational basis with a new basis that depends on the operation that we want to perform. Probabilistic measurements are also described by matrices, but these matrices are hermitian, so in ket notation, they are just weighted sums of these ket-bra terms, where the psi_k states form an orthonormal basis for the space.
Readout \(\equiv\) measurement operators \(\equiv\) hermitian matrices
If a measurement results in the state \(\psi_{k}\), the value \(r_{k}\) becomes known to the experimentalist.
The expected value for this measurement is given by sandwiching the measurement operator with the state that we’re measuring, and as you can see, the expectation value is just a weighted sum of the \(r_{k}\) terms, with the probabilities given by Born’s rule.
Average experimental outcomes \(\equiv\) ‘sandwich’ prodducts
6.1.1. Unitary operations
That’s probably a lot to take in all at once, so let’s take a look at a few examples. Here, we have a unitary operation that exchanges states in the computational basis, which we call X, or the Pauli X if you’re already familiar with Pauli matrices. $\( X=\left[\begin{array}{cc} 0 & 1\\ 1 & 0 \end{array}\right]=\mid1\rangle\langle0\mid+\mid0\rangle\langle1\mid\,\,\,\,\,X\mid0\rangle=\mid1\rangle\,\,\,\,\,X\mid1\rangle=\mid0\rangle \)$
Here it is decomposed into ket-bra terms, and here’s what happens when we use it to transform one of the computational basis states. We just get the other state. 0 goes to 1, and 1 goes back to 0. Not so exciting. Now let’s take a look at a more interesting operation, the Hadamard gate, H.
As you can see, this changes the basis from the 0/1 basis to the +/- basis that we discussed earlier. Put in a 0, get out a +, put in a 1, get out a -. There is another gate, called the phase gate, which only multiplies the one state by a factor of i, changing the basis in a very subtle way. $\( P=\left[\begin{array}{cc} 1 & 0\\ 0 & i \end{array}\right]=\mid0\rangle\langle0\mid+i\mid1\rangle\langle1\mid\,\,\,\,\,P\mid0\rangle=\mid0\rangle\,\,\,\,\,P\mid1\rangle=\mid1\rangle \)$
Now let’s take a look at a few measurement operators. In an interesting coincidence, the Pauli X shows up again, since it’s both unitary and hermitian, we can use it both as an operation and a measurement.
Hermitian observables: $\( X=\left[\begin{array}{cc} 0 & 1\\ 1 & 0 \end{array}\right]=\mid+\rangle\langle+\mid-\mid-\rangle\langle-\mid\,\,\,\,\,\langle+\mid X\mid+\rangle=1\,\,\,\,\,\langle-\mid X\mid-\rangle=-1 \)$
Here, we have decomposed it into its eigenbasis, so the ket-bra terms are different than before, and we can see that its output values are +/- 1. Here’s another matrix which is both unitary and hermitian, the pauli Z. $\( Z=\left[\begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}\right]=\mid0\rangle\langle0\mid-\mid1\rangle\langle1\mid\,\,\,\,\,\langle0\mid Z\mid0\rangle=1\,\,\,\,\,\langle1\mid Z\mid1\rangle=-1 \)$
It returns the exact same values as X, just for states in the 0/1 basis instead of the +/- basis.
And finally we have the identity, which is also unitary and hermitian.
We can note that the identity doesn’t change the basis at all, so that indeed it can be expressed in any basis. Also when used as a measurement operator, it always returns 1, no matter what state is input.
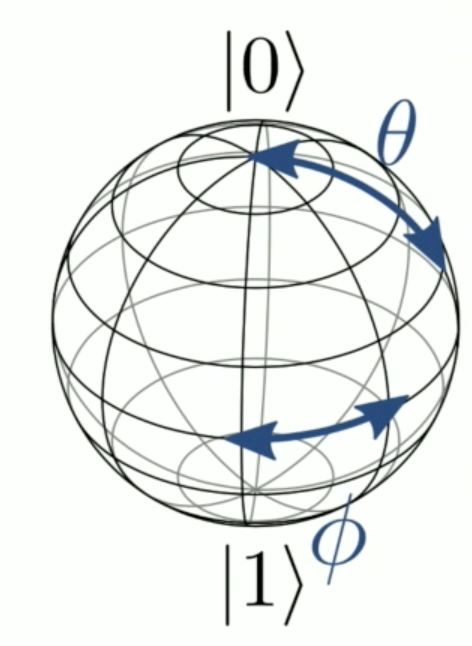
6.1.2. The Bloch Sphere
Coefficient in polar co-ordinates:
normalization constrains qubits’ states further
Now that we have a few examples done, I would like to focus a little on a useful geometric representation of qubit states, called the Bloch Sphere. To show how qubit states can be mapped to the surface of a sphere, let’s start by expressing the coefficients alpha and beta in polar co-ordinates.
Next, we can note that we can get rid of the phase on the alpha coefficient, since a ket multiplied by a phase produces the same measurement results as the ket itself, for any potential experiment, so these are not different in any physical sense.
(global phases don’t matter??
This results in a simpler expression for the state, but it’s not yet as simple as it can be.
To get it even simpeler, we need to recall that these states have to be normalized, so the sum of the squares of the two radii involved has to be 1.
This implies that we can express them as the cosine and sine of an angle theta, since cos(theta)^2 + sin(theta)^2 is always 1.
This family of angles theta and phi also describes the set of points on the surface of a sphere of unit radius in 3d space.
If we set theta to \(\pi\) however, we get the 1 state regardless of the setting of phi. Likewise if we set theta to \(pi/2\), and \(\phi\) to either \(0\) or \(\pi\), we get one of the states from the \(+/-\) basis on the equator of the sphere.
Unitary operations, which change the basis we are working in, effect1ively rotate the sphere. For example, the Hadamard operation from earlier rotates the +/- states on the equator by 90 degrees until they’re at the poles. Also note that the states on opposite sides of the sphere are actually orthogonal, so this mapping does not preserve the angle between states, but it’s still useful for describing single-qubit states and operations.
Unitary operations rotate the sphere $\(\left\langle \psi\mid\psi^{\prime}\right\rangle =0\leftrightarrow\text{anti-parallel on the Bloch sphere}\)$
But how do we describe multi-qubit states and operations? Specifically, how do we build them up from operations on smaller subsystems of a many-qubit state? To accomplish this, we use a different kind of matrix product, called the tensor product, or Kronecker product. To take the tensor product of two matrices A and B, we write out a block matrix where each block is equal to B times the appropriate element of A.
Multi-qubit states and operations: tensor (or Kronecker) products:
The upper left block is B times the upper left element of \(A\), and so on.
The interesting thing about the tensor product is that it’s compatible with the regular matrix product.
That is to say if I take the matrix product of two tensor products, I get the same matrix as if I took the matrix products first, then evaluated the tensor product. This is also easier to understand if we take a look at a few examples.
7. Multi-Qubit States & Operations
Here we see the tensor product of two states, + and 0, resulting in a state which we often call +0. Each 2-by-1 block of the state vector we’re calculating is proportional to the vector for the zero state, and it’s multiplied by one of the elements of the plus state.
We can also take tensor products of operations and observables, here we take the tensor product of X and the identity, making a block matrix whose blocks are all equal to the identity, multiplied by one of the elements of X.
7.1. Example: Bell State Preparation
Now that we have seen the basic formalism and notation, we’re ready to calculate the results of a small sequence of quantum operations, which prepares a Bell state. First, we introduce a two-qubit gate which cannot be written as a tensor product of one-qubit gates, the controlled not, or cnot for short.
As we can see, it can be decomposed into a sum of two tensor products that says if the first qubit is in the zero state, do the identity, and if the first qubit is in the one state, perform an X on the second qubit. Here we see the Bell state, which we’re going to prepare using the cnot.
We can write it out using either ket notation, or as a column vector.
7.2. Example: Bell State Preparation
Note that the Bell state, just like the cnot, cannot be written as a tensor product. The first step in preparing the Bell state is to perform a Hadamard operation on the first qubit, which has been initiliazed in the zero state. So we calculate the tensor product of the Hadamard with the identity, since we’re not going to do anything to the second qubit immediately.
Now we’re ready to set up our sequence of operations. First, we prepare the state 00, then we apply the Hadamard, then the cnot. This results in a Bell state, which is written out here as a column vector.
Now this is the correct answer, but it was a little tedious to come to, and the matrices involved are a little large. 3x3 matrices are typically big enough for any phisicist, so 4x4 is overdoing it a little.
Let’s try and do it the easy way, using some more ket notation. First, we use the compatibility of the Kronecker and regular products to show that the state we get from executing the Hadamard on the first qubit is simply +0, without having to use any matrices.
Now, all we have to show is that the cnot will take our state, which is 00 + 10, to the 00 + 11 state that we’re after.
If we insert the decomposition of the cnot into tensor products that we saw earlier, we can see that the resulting state has coefficients proportional to these inner products of the 0 & 1 states.
Of course, the 0/1 basis is orthonormal, so the products 00 and 11 evaluate to 1, and the products 01 and 10 evaluate to 0, leaving us with two remaining terms.
These terms are exactly the 00 and 11 terms that we were after. And that’s how ket notation van help us to describe the effects of operations and measurements on quantum states.
7.2.1. Main takeaways
In ket notation, a quantum state is expressed using a column vector with complex coefficients. The squared magnitudes of these coefficients are the probabilities of measuring that particular outcome.
Devices used for storing and manipulating qubit states are described by a Hamiltonian, which is a matrix that assigns energies to each of its eigenstates or preferred basis states.
Quantum logic gates are described by unitary matrices. Probabilistic measurements are described by Hermitian matrices.
An entangled state is a multi-qubit state that cannot be written as a tensor product of one-qubit states.
Qubit states are geometrically represented using the Bloch sphere.
Multi-qubit states and operations can be described using the tensor product. Note, an actual two-qubit gate cannot be described with a tensor product.
8. Advantages and dissadvantages of Ket notation
In the previous ket notation we discussed three ways to represent quantum states:
column vectors with complex coefficients,
kets themselves and
the geometric representation,
which uses the Bloch sphere. Each one of these has their own little advantages and disadvantages, which we are going to see in the course of these videos. First, let’s take a look at some of the advantages of ket notation. So here’s ket…notation. Is very nice for…sparse…states. That is to say: states… …which don’t have that many non-zero entries in some bases. Take for example this state here, which I will call psi, along with most other states.
It has got two nonzero terms. There is a one over root two term for the component in \(00000\) and a one over root two term for the all-ones as well. That would be very cumbersome to write out in terms of a full vector, because that would require \(2^5\) or \(32\) entries, but here you can do it very compactly. Now, if you don’t have a compact discription for the state like this, if you just have some arbitrary coefficients, it can be very painstaking and time-consuming to write out something like this.
\(\beta\otimes 01 + \gamma \otimes 10 + \delta \otimes 11\). Here you would be better of to use something more like a column vector. \(\alpha, \beta, \gamma, \delta\).
And in some other times, especially if you’re considering operations - transformations on the set of states – it can be beneficial to consider the Bloch sphere, where you have the reference state zero, some other states one, plus, minus and like so…
8.1. Synthesising rotations
In some setups, experimentalists can only rotate along two axes of the Bloch sphere. In this video Ben will show you an example of how you can use these two rotation axes to achieve rotations around a third axis. He will do it both in vector form and in the Bloch sphere representation. Which do you think is the most convenient?
Let’s show an example of something that’s a little bit difficult to do when looking at the matrix based picture of quantum mechanics, but if we put everything on the Bloch sphere it makes perfect sense.
In many experiments, experimentalists can only rotate along two axes of the Bloch sphere. That is the x-axis, which goes in this direction and the y-axis, which is going in this way.
Many algorithms rely on rotations around the z-axis, which is independent from these other two. And we would like to see how to synthesize the z-rotations out of the tools that we have available: x and y rotations.
Now, I happen to know the answer to this question and I can begin by writing down the matrices that describe the operations that we would like to do. So, here is z and I’ll say this is z(theta). For those of you who are really in the know, this is
and
on the diagonal, zeros off the diagonal. And we can see immediately that x and y rotations on their own aren’t going to give us this z-rotation.
So we can write down x theta and y theta, which are just rotations around these axes by angles theta.
And this guy is equal to cosine of theta over two minus i \(sin(\frac{\theta}{2}) -i\sin(\frac{\theta}{2})\)
is quite similar. Cosine theta over two, sine theta over two, minus sine theta over two, cosine theta over two. Now, there’s a product of these rotations. A y an x and a y, that will excecute one of these sets.
Lets look at those matrix rotations first. What I am going to do is set theta, well, equal to pi over two for a y rotation. And that’s going to give me one over root two, one one, minus one, one. Y theta equal to minus pi over 2 will give me operations that look like one, minus one, one, one. You might recognize these to be quite similar to the Hadamard matrix that changes from the computational basis to the plus minus basis, and that is by design.
Now lets take a look at what happens if we sandwich an x rotations around theta with these two matrices, which we lovingly call y 90 and y -90. Because they are 90 degree rotations. So, we’re going to get a, well, y pi by 2 x theta y minus pi 2. Is equal to 1 over root two one, minus one, one,one, cosine theta over two, minus i sine theta over two, minus i sine theta over two, cosine of theta over two. Then we have another one over root two, one, minus one, one, one. We multiply these through. So, first off I can take these two factors of one over square root of two, make them a factor of a half. One minus one one one. Then if I multiply these here, I get cos theta over two plus I sine theta over two, because these two minus signs cancel. So that’s cos theta over two plus I sine theta over two.
Here I’ll get cosine theta over two minus I sine theta over two. Here I’ll get minus cosine, minus I sine. So that’s minus I cosine theta plus I sine theta over two. And then here I’ll get cosine minus I sine. So, cosine theta over two minus I sine theta over two. Continuing on with all this math I can notice that these two elements are equal and opposite. So If I take one and minus one, I’ll get cosine plus I sine, minus negative cosine plus I sine. Which is simply two cosine theta over two plus I sine theta over two. Here I take a number and it’s opposite, I get zero. Here I can take these two numbers which are equal and add them. That gives me theta over two minus I sine theta over two. And if I take one and minus one and these two I get zero as well.
That’s a lot of matrix multiplication. Now, let’s also use Eulers identity. We know that this is equal to e^{itheta/2} and that this is equal to e^{-iTheta/2}.
So by using a little bit of ket notation and some trigonometric identities, we can show that we can obtain universal control using only the tools that are available to the experimentalists. This is nice because it means we don’t have to design new hardware. We can just put together operations that we already have in order to obtain universal control.
But this is not that simple as it could be. There is a far easier way to see this, which we can do using the Bloch sphere. The action of this sequence of unitary operations. Y 90, x around some angle theta and then y minus 90 can be expressed in terms of matrices. But it’s much easier to see using the Bloch sphere. If we write down the Bloch sphere with the x axis pointing out of the board, we can see the effect of a y 90, a rotation around 90 degrees of the y axis, is just turning the sphere sort of like a steering wheel, so that the x axis now faces down and the z axis is where the x axis used to be. If we now apply a rotation around the x axis, that is giving us a rotation around our old z axis. And once we have that done, all we have to do is reverse the y 90 with a y minus 90 to restore the orientation of our original axes, having picked up a phase on the z. And that’s how we can synthesize a diagonal unitary. e^{itheta/2}, e^{-i*theta/2} out of the operations to which the experimentalists have access. A little bit of notations saves you a lot of hardware design.
8.2. State decomposition
Often in quantum computing , it is necessary to express one state in terms of a basis of some other states. I am going to go ahead and call this state decomposition, although you can see it under a variety of names and usually it’s clear from the context that they mean expressing one state in terms of a basis that is more familiar or convenient to. Now the rule of state decomposition is that any state phi can be expressed as a sum over k terms, where each term consists of an inner product of phi - the trial state - with one of the basis states phi_k, and the states phi_k. Number times vector. And this is the same as decomposing a vector in a basis if you are already familiar with linear algebra.
As an example of this, let’s take a look at a trial wave function of zero, and a basis which is the Hadamard basis, the plus minus basis, that we reviewed in the lecture. The sum over psi_k, phi, psi_k is then the inner product of plus and zero times plus and the inner product of minus and zero times minus. Now here I figured out those inner product. The inner product of plus zero is one over root two times the dot product of these two vectors, which is just one over root two. And the calculation for minus zero is very similar, there is a minus sign here, but it gets multiplied by zero, making no difference, and we end up with one over root two again. Therefore, zero can be decomposed as one over root two, plus + minus, just as the plus state can be decomposed as one over root two, zero + one.
Example:
8.3. Performing arbitrary measurements
It could be that your measurement device is only capable of measuring in one basis. Ket notations helps us to show that it will not be difficult to let this simple measurement device measure in any basis. In this example Ben will show you how this works.
I’d like to talk today about how a little bit of ket-notation can save us a big experimental headache, when it comes time to try measure a qubit in an arbitrary basis. First, we have to review a few of the important facts.
Arbitrary measutremnent
The conjugate transpose of a matrix or a vector is given by first taking the transpose of this 2-by-2 matrix that leaves the diagonal elements in the same place, and exchanges the elements being b and c here, but also taking the complex conjugate of each element in the matrix.
A second important fact, which you can prove yourself using this definition, and I encourage you to do so, is that the dagger or complex conjugate transpose of U- psi (ket) is just the bra for psi times U-dagger. Now, that follows from linear algebra, but it is easy to check for yourself.
There’s also another construction that I’d like to use, which is that for every state psi, there is another state which I call psi-perp(endicular), which consists of these coefficients. So, if psi is alpha-beta, psi-perp is the conjugate of beta and minus the conjugate of alpha. And these states are by construction orthogonal, which you can also see just by taking the inner product and seeing that it’s always zero regardless of what alpha and beta are.
And with those three ingredients, we can solve this question.
´+ So, experimentalists usually measure a single operator: the Pauli-Z operator, that was perhaps discussed earlier. But we’d like to be able to measure in whatever basis we want.
So that if we have a question: “Is this state this or that?”, we can answer it without having to restrict ourselves to the 0-1 basis. So, we have a two-step plan to solve this. First, we’re going to apply some operator U, and then we’re going to measure in the 0-1 basis.
+How to measure in other basis
Apply U
Measure in {\mid0\rangle,\mid1\rangle\rangle
Now, if you’ve got a controllable qubit, you can apply an operator U as you see fit, and as discussed in the statement of the question, we can measure in the 0-1 basis. We can measure the Z-operator. So, the expectation value of this measurement, if we first apply U on psi, that replaces psi with psi-U-dagger in the bra and U-psi in the ket, and then we take the familiar sandwich product to determine the expectation value of the operator, we end up with psi-U-dagger-Z-U-psi.
Expectation value;
So, it’s as if we had our original state psi, and instead of measuring Z, we measured U-dagger-Z-U. Now, U-dagger-Z-U we can write out like so. And if we label the state U-dagger-0 as psi, then U-dagger-Z-U is equal to psi-psi minus psi-perp-psi-perp. This is a measurement that will return 1 if the state is psi, and -1 if the state is psi-perp, giving us an arbitrary basis to measure in.
9. A fact about maximally entangled states
Ket notation is not always the best approach to find an answer or solve an equation. Ben will give you an example about entangled states where it would be a lot of work to use ket notation.
Often when doing quantum information, ket-notation can fail you. This happens a lot when you have a densely packed vector full of a bunch of different coefficients and there’s no obvious structure. Now, hopefully when that happens to you, you’re only going to deal with a few qubits. Otherwise, you are going to writing out coefficients for a very long time.
Here, we can see a not too bad example with two qubits where we’re going to prove that for any maximally entangled state of the form psi-star-psi plus psi-perp-star-psi-perp, it’s always equal to the Bell state that’s fully correlated that we know and love: 1 over root 2 (times) 0-0 plus 1-1.
And this is regardless of what psi is. So, if we take an arbitrary wavevector psi which is two complex coefficients alpha and beta, we can define psi-star, which is just the complex conjugate of that state, which is also a valid state, psi-perp, which is some state which is orthogonal to psi, which I encourage you to check for yourself by taking the inner product, and psi-perp-star, which is the complex conjugate of the orthogonal state. And if we write out all of our tensor products using the formula that we learned earlier, we obtain a pair of densely packed vectors full of those coefficients, which would be very awkward in ket-notation.
But we have here alpha-star-alpha, alpha-star-beta, beta-star-alpha and beta-star-beta. And we’re going to add to that: beta-beta-star, minus beta-alpha-star, minus alpha-beta-star and alpha-alpha-star. Now, beta-star-beta plus alpha-alpha-star is just the magnitude of alpha squared plus the magnitude of beta squared, which is 1. And we see that same thing in the top term here, alpha-star-alpha plus beta-beta-star, that’s 1. And then these inner terms cancel. Because you have alpha-star-beta minus beta-alpha-star, that has just been flipped here. And a beta-star-alpha minus alpha-beta-star, if I flipped these two, it becomes obvious that they are equal and opposite, so they cancel. This implies for example, that for example if Alice and Bob share a Bell state, and Alice measure in a 0-1 basis, she can get a state 0 or 1 and she can tell that Bob has the same state. Now she measures instead in the basis psi-star psi-star-perp, she can tell that Bob has the state psi or psi-perp depending on her measurement result.
10. Experimental and theoretical measurements
In this section we will explain the difference between measurements that occur in a laboratory and measurements that are described in theory. What are the differences and how are those similar?
Let’s take this opportunity to clarify something that confuses a lot when first learning about quantum mechanics, which is the difference between measurements that occur in a laboratory and measurements that we describe in theory. And also point out hopefully the ways in which these things are similar. So, you may have already seen a picture like this one. But, in the laboratories we can measure some currents in nanoamperes, and if there’s a spin in the down state pointing parallel to the field, there will be no bump in the current. And if it’s in the up state, there will be a bump. And this is a large macroscopic classical signal that they can detect. And this relates to a measurement operator. You can imagine that we take the total area under this curve; the total amount of current, in the case that there’s no bump, and that corresponds to the spin down state. And the total current in the case that there is a bump will be slightly higher, and that corresponds to the spin up state. So, that real number: the amount of current times the projector on to the down state plus the total amount of current in the case that there is bump times the projector on to the up state gives us our measurement operator. Now, the important thing about these two signals being distinguishable, but there being a large difference between them, is that if they’re equal, we end up with some number times down-down plus some number which is identical, times up-up. So, the measurement operator becomes the identity, which doesn’t discern between the up and down states. So as useless is the measurement. But if these numbers are discernably different, then down-down and up-up receive different measurement outcomes, and out measurement operator is \mathbf{1}more like a Z, which is one we could use to accurately distinguish between the computational basis states in quantum computing.
10.1. Practice Quiz 3
10.1.1. Question 1:
Suppose we are given a pure, two-qubit state $\(\psi\rangle_{AB}=\alpha_{00}|00\rangle+\alpha_{01}|01\rangle+\alpha_{10}|10\rangle+\alpha_{11}|11\rangle, where \left|\alpha_{00}\right|^{2}+\left|\alpha_{01}\right|^{2}+\left|\alpha_{10}\right|^{2}+\left|\alpha_{11}\right|^{2}=1 \)\(. We can compute the amount of entanglement between the two qubits, as quantified by the entanglement measure known as the concurrence, using the following expression: \)\(C\left(|\psi\rangle_{AB}\right)=2\left|\alpha_{00}\alpha_{11}-\alpha_{01}\alpha_{10}\right\mid\)\(. If the two qubits are maximally entangled, then \)\(C(|\psi\rangle)=1\)\(; and if the qubits are not entangled at all, or are in a product state, then \)\(C(|\psi\rangle)=0\)$. Use the above expression to compute the amount of entanglement between the qubits in each of the following states:
how much entanglement is in that state?
[] \(\mid\psi\rangle_{AB}=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)=\mathbf{1}\)
[] \(\psi\rangle_{AB}=\frac{1}{\sqrt{2}}(|01\rangle+|10\rangle)=\mathbf{1}\)
[] \(\psi\rangle_{AB}=|00\rangle=\mathbf{0}\)
\(\psi\rangle_{AB}=\sqrt{\frac{48}{100}}(|00\rangle+\sqrt{\frac{48}{100}}|11\rangle)+\sqrt{\frac{4}{100}}\mid10\rangle=\mathbf{0.96}\)
Explanation
Without a programming language, every input into the computer would need to be an exact instruction on the CPU. This would make using computers very hard and would take a lot of time.
0 points possible (ungraded)
10.2. Quiz 3: Ket notation
10.2.1. Question 1: Expectation values
The expectation value \(\langle A\rangle\) of an operator \(A\) upon a state \(\mid\psi\rangle\) is, as mentioned, the average of very many outcomes of measurements of that operator. Mathematically speaking, it is the inner product of the state with itself, with the operator ‘sandwiched’ inbetween: \(\langle\psi|A|\psi\rangle\).
The easiest way to solve this is using the linear algebra representation: if, for instance, $\( A = \left[\begin{array}{ccc} 1 & 0\\ 0 & -1 \end{array}\right], and |\psi\rangle equals \left[\begin{array}{l} 1\\ 0 \end{array}\right], then: \langle\psi|A|\psi\rangle=\left[\begin{array}{ll} 1 & 0\end{array}\right]\left[\begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}\right]\left[\begin{array}{l} 1\\ 0 \end{array}\right] For the state \sqrt{\frac{1}{3}}|0\rangle+\sqrt{\frac{2}{3}}i|1\rangle\)$
calculate the expectation value of the following operators:
10.2.1.1. Hadamard matrix:
Complex conjugate transpose: $\( \langle\psi\mid=\mid\psi*\rangle=\sqrt{\frac{1}{3}}|0\rangle-\sqrt{\frac{2}{3}}i|1\rangle=\left[\begin{array}{cc} \sqrt{\frac{1}{3}} & -\sqrt{\frac{2}{3}}i\end{array}\right] \)$
10.2.1.2. Pauli X
10.2.1.3. Pauli Y matrix
10.2.1.4. Pauli Z matrix:
10.2.1.5. Question 2: Entanglement between qubits
An entangled state is a multi-qubit quantum state that can not be written as a Kronecker product of single-qubit states.
For example, if we take the tensor product of two arbitrary states |\psi\rangle=\left[\begin{array}{l}
If we are given a vector, such as
and we want to show that it is separable (unentangled), we need to find a set of numbers \(\{\alpha,\beta,\gamma,\delta\}\) such that \(\alpha\gamma=1,\alpha\delta=0,\beta\gamma=0\), and \(\beta\delta=0\). The assignment \(\alpha=\gamma=1\), \(\beta=\delta=0\) accomplishes this, and we can say that the state is \(\mid0\rangle\otimes|0\rangle\), and therefore separable. If such an assignment does not exist, then the state is entangled. Mark all states below that are entangled:
how much entanglement is in that state?
[] \(\mid\psi\rangle=\sqrt{\frac{1}{4}}\left[\begin{array}{l} 1\\ 1\\ 1\\ 1\end{array}\right]\)
\(\mid\psi\rangle=\sqrt{\frac{1}{4}}\left[\begin{array}{l} 1\\ 1\\ 1\\ 1 \end{array}\right]\)
[] \(\mid\psi\rangle=\sqrt{\frac{1}{2}}\left[\begin{array}{l} 0\\ 0\\ 0\\ 0\\ 1\\ 0\\ 0\\ 1 \end{array}\right]v\)
\(\mid\)
[] \mid\psi\rangle=\sqrt{\frac{1}{2}}\left[\begin{array}{l} 0\ 0\ 1\ 0\ 0\ 0\ 1\ 0 \end{array}\right]
[] \mid\psi\rangle=\frac{\mid00\rangle+\mid10\rangle}{\sqrt{2}}
\mid\psi\rangle=\frac{\mid00\rangle+\mid11\rangle}{\sqrt{2}}
\mid\psi\rangle=\frac{\mid++\rangle+\mid–\rangle}{\sqrt{2}}
Explanation
Following the method from the hints, the state $\(\sqrt{\frac{1}{4}}\left[\begin{array}{l} 1\\ 1\\ 1\\ 1 \end{array}\right] has coefficients a_{00}=a_{01}=a_{10}=a_{11}=\frac{1}{\sqrt{4}}\)$
So if we write out the kronecker product, we see that
\(\alpha^{*}\gamma,\alpha^{*}\delta,\beta^{*}\gamma\) and \(\beta^{*}\delta\) should all be equal to \(\frac{1}{\sqrt{2}}\).
This is easily the case for \(\alpha=\beta=\gamma=\delta=\frac{1}{\sqrt{2}}\). We can conclude that we can write this state as \((\alpha|0\rangle+\beta|1\rangle)\otimes(\gamma|0\rangle+\delta|1\rangle)\) with \(\alpha=\beta=\gamma=\delta=\frac{1}{\sqrt{2}}\), so the state is not entangled. If we try to write $\(\mid\psi\rangle=\sqrt{\frac{1}{3}}\left[\begin{array}{l} 1\\ 0\\ 1\\ 1 \end{array}\right\)\( as a kronecker product, we see that \)\alpha^{}\delta=0\(, but that \)\alpha^{}\gamma=\beta^{*}\delta=\frac{1}{\sqrt{3}}$. This is a direct qubit states, and is thus entangled.
10.2.1.6. Question 3: Two-qubit operations
2 qubit operations are operations that involve, as expected, 2 qubits. Just as 1 qubit operations they can be written in matrix form. However, since 2 qubits are now involved, these matrices are now 4\times4 unitaries. For the following 2 qubit operations, click the appropiate matrix that corresponds with the operation. - The 2 qubit operation that applies a bit flip on the second qubit, conditioned on the first qubit being in the \(\mid1\rangle\) state. So, a bit flip is applied to the second qubit if the first qubit is in the \(\mid1\rangle\) state, and no flip is applied if the first qubit is in the \(\mid0\rangle\) state. A bit flip (or X ) turns a 0 into a 1 and a 1 into a 0 . so
Calculating this product results in the desired matrix.
### Question 4: Unitaries, or mapping one basis to another
Let the basis
$$\{\mathbf{v}\} be the set of vectors \left\{ \left[\begin{array}{c}
\cos\theta_{1}\\
\sin\theta_{1}
\end{array}\right],\left[\begin{array}{c}
-\sin\theta_{1}\\
\cos\theta_{1}
\end{array}\right]\right\}
$$
And let the basis
$$\{\mathbf{b}\} be the set of vectors \left\{ \left[\begin{array}{c}
\cos\theta_{2}\\
\sin\theta_{2}
\end{array}\right],\left[\begin{array}{c}
-\sin\theta_{2}\\
\cos\theta_{2}
\end{array}\right]\right\}
$$
Calculate the matrix that maps $\{\mathbf{b}\}$ to $\{\mathbf{v}\}$. To input the questions, fill every 4 entries in seperately below. Simplify answers as good as possible by using these identities.
$$
\begin{array}{|l|}
\hline \operatorname{Product-to-sum}\\
\hline \cos\theta\cos\varphi=\frac{\cos(\theta-\varphi)+\cos(\theta+\varphi)}{2}\\
\sin\theta\sin\varphi=\frac{\cos(\theta-\varphi)-\cos(\theta+\varphi)}{2}\\
\sin\theta\cos\varphi=\frac{\sin(\theta+\varphi)+\sin(\theta-\varphi)}{2}\\
\cos\theta\sin\varphi=\frac{\sin(\theta+\varphi)-\sin(\theta-\varphi)}{2}\\
\tan\theta\tan\varphi=\frac{\cos(\theta-\varphi)-\cos(\theta+\varphi)}{\cos(\theta-\varphi)+\cos(\theta+\varphi)}\\
\hline \prod_{k=1}^{n}\cos\theta_{k}=\frac{1}{2^{n}}\sum_{e\in S}\cos\left(e_{1}\theta_{1}+\cdots+e_{n}\theta_{n}\right)\\
\text{ where }e=\left(e_{1},\cdots,e_{n}\right)\in S=\{1,-1\}^{n}\\
\prod_{k=1}^{n}\sin\theta_{k}=\frac{(-1)^{\left\lfloor \frac{n}{2}\right\rfloor }}{2^{n}}\left\{ \sum_{e\in S}\cos\left(e_{1}\theta_{1}+\cdots+e_{n}\theta_{n}\right)\prod_{j=1}^{n}e_{j}\text{ if }n\right.\text{ is even, }
\\\hline \end{array}
$$
$$
\begin{aligned} & \text{ Sum-to-product }{}^{[28]}\\
& \sin\theta\pm\sin\varphi=2\sin\left(\frac{\theta\pm\varphi}{2}\right)\cos\left(\frac{\theta\mp\varphi}{2}\right)\\
& \cos\theta+\cos\varphi=2\cos\left(\frac{\theta+\varphi}{2}\right)\cos\left(\frac{\theta-\varphi}{2}\right)\\
& \cos\theta-\cos\varphi=-2\sin\left(\frac{\theta+\varphi}{2}\right)\sin\left(\frac{\theta-\varphi}{2}\right)\\
& \tan\theta\pm\tan\varphi=\frac{\sin(\theta\pm\varphi)}{\cos\theta\cos\varphi}
\end{aligned}
$$
A nice video that explains transformations of bases can be found here. Fill in
$$\cos\theta_{1} as \cos\left(\right. theta_1) \cos\left(\theta_{1}+\theta_{2}\right)$$ as
$$\cos (theta_1 + theta_2), \cos\theta_{1}\cos\theta_{2} as \cos\left(\right. theta_1)$$
$$\cos ($ theta_ 2$), \cos \theta_{1}+\cos \theta_{2}$$
as
$$\cos ($ theta_1 $+$ $\cos$ (theta_2)$$, etc. Also, answers provided in the most compact form: $$\sin \left(\theta_{1}+\theta_{2}\right)$$ or similar are preferred as others might raise problems in being detected as correct even if they are. Remember and use these identities:
$$\sin\left(\theta_{1}\pm\theta_{2}\right)=\sin\left(\theta_{1}\right)\cos\left(\theta_{2}\right)\pm\cos\left(\theta_{1}\right)\sin\left(\theta_{2}\right)$$
$$\cos\left(\theta_{1}\pm\theta_{2}\right)=\cos\left(\theta_{1}\right)\cos\left(\theta_{2}\right)\mp\sin\left(\theta_{1}\right)\sin\left(\theta_{2}\right)$$
```{admonition} Explanation
Hint (1 of 3): Since it is a mapping from one basis to another, the matrix should be unitary.
Hint (2 of 3): You can use a geometrical argument to solve this
Hint (3 of 3): The top left entry is the inner product between \boldsymbol{v}*{1}and \boldsymbol{b*{1}:}\langle\boldsymbol{v_{1}}\mid\boldsymbol{b_{1}}\rangle
The top left entry in the matrix is:
- [x] $cos(theta_{1}-theta_{2})$$
$$ cos(theta_1 - theta_2) or cos(theta_2 - theta_1) or cos(theta_1)cos(theta_2) + sin(theta_1)sin(theta_2) or cos(theta_1-theta_2) or cos(theta_2-theta_1) or cos(theta_1)cos(theta_2)+sin(theta_1)sin(theta_2) or cos(theta_2)cos(theta_1) + sin(theta_2)sin(theta_1) or cos(theta_2)cos(theta_1)+sin(theta_2)sin(theta_1)$$
The top right entry in the matrix is:
- [x] $sin(theta_{1}-theta_{2})$
$$ sin(theta_1 - theta_2) or sin(theta_2 - theta_1) or cos(theta_1)sin(theta_2) - sin(theta_1)cos(theta_2) or -sin(theta_1-theta_2) or sin(theta_2-theta_1)$$ or
$$cos(theta_1)sin(theta_2)-sin(theta_1)cos(theta_2) or sin(theta_2)cos(theta_1)-cos(theta_2)sin(theta_1) or sin(theta_2)cos(theta_1) - cos(theta_2)sin(theta_1)$$
The bottom left entry in the matrix is:
- [x] sin(theta_{1}-theta_{2})
sin(theta_1 - theta_2) or -sin(theta_2 - theta_1) or sin(theta_1)cos(theta_2) - cos(theta_1)sin(theta_2) or sin(theta_1-theta_2) or -sin(theta_2-theta_1) or sin(theta_1)cos(theta_2)-cos(theta_1)sin(theta_2) or cos(theta_2)sin(theta_1) - sin(theta_2)cos(theta_1) or cos(theta_2)sin(theta_1)-sin(theta_2)cos(theta_1)
The bottom right entry in the matrix is:
- [x] cos(theta_{1}-theta_{2})
$$ cos(theta_1 - theta_2) or cos(theta_2 - theta_1) or cos(theta_1 - theta_2) or cos(theta_2 - theta_1) or cos(theta_2-theta_1) or cos(theta_1-theta_2)$$
**Explanation:** The inner product between \boldsymbol{v_{1}\,}\text{and}\,\boldsymbol{b_{1}}\rangleis cos(𝜃1)cos(𝜃2)+sin(𝜃1)sin(𝜃2). Using the identities in the link, this can be written as cos(𝜃1−𝜃2). The rest of the inner products can be calculated the same way. Note that the answer only depends on the difference between $\theta_{1}$ and $\theta_{1}$!